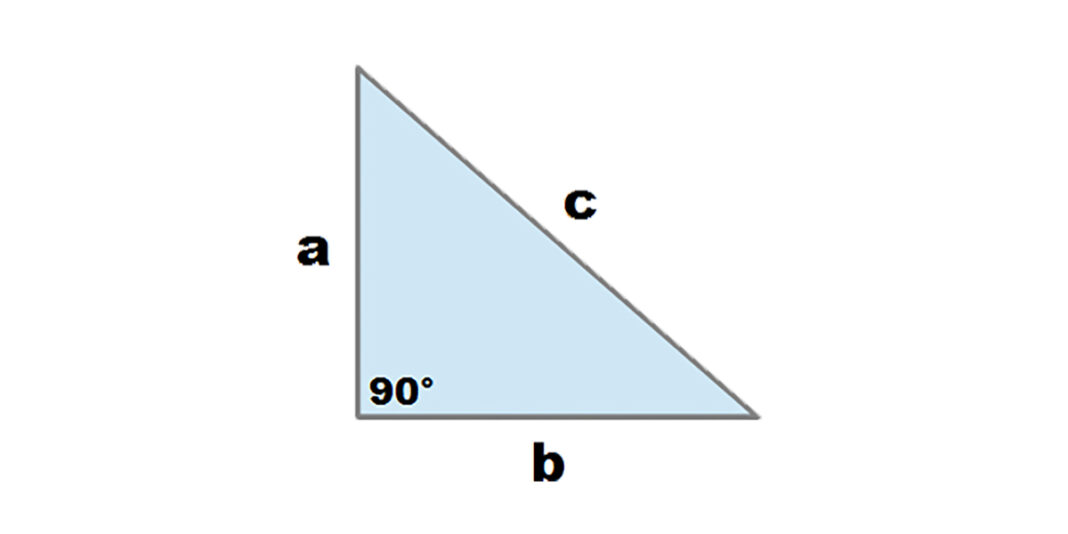
Un triangolo è definito come una figura geometrica con tre lati e, conseguentemente, tre angoli. Esistono varie classificazioni di triangoli (equilatero, isoscele, ecc.) e, specificatamente per questo articolo, ci concentreremo sul triangolo retto, che si distingue per la presenza di un angolo di 90 gradi. Esploriamo come determinare la misura degli angoli di un simile triangolo, considerando anche alcuni fondamenti base della geometria bidimensionale.
Triangolo retto: nozioni fondamentali
Abbiamo già delineato che un triangolo è catalogato come retto se uno dei suoi tre angoli ha una misura di 90°. Il lato che si trova di fronte a questo angolo è chiamato ipotenusa, mentre i rimanenti due lati vengono definiti come cateti.
È importante tener presente che in qualsiasi triangolo, la somma degli angoli interni è di 180°. Da questa regola si deduce facilmente che un angolo è di 90°, e così è la somma del rimanente paio.
Misurazione dell’Angolo Tramite l’Uso dell’Arcotangente
Siamo giunti alla conclusione, con assoluta certezza, che i due angoli, che non sono retti, sommano 90°. In questa circostanza, la nozione di arcotangente può essere fondamentale. Infatti, sfruttando la relazione che intercorre tra i lati, noti come cateti, possiamo determinare l’angolazione dei vari angoli.
Per ottenere il risultato si applica la seguente equazione: angolo più piccolo = arcotangente (cateto minore/cateto maggiore).
In altre parole, per misurare l’angolo che si forma tra l’ipotenusa e il cateto maggiore, divide la tangente del cateto maggiore per quella del cateto minore.
Una volta ottenuto questo parametro, tramite una semplice sottrazione, è possibile determinare il valore dell’angolo rimanente.
Esistono specifiche formule trigonometriche per calcolare l’arcotangente, tuttavia, risulta più facile e sicuro utilizzare una calcolatrice scientifica che, tra le altre funzioni, permette di calcolare l’arcotangente.
Determinare l’ampiezza tramite incognite
Ci può capitare di incappare in varie categorie di informazioni. Per essere più precisi, potrebbe essere dato, ad esempio, che un inclinazione supera un altro di 10°. In tal caso, possiamo disvelare il mistero utilizzando un insieme di variabili sconosciute, prendendo sempre come riferimento i dati concreti e certi in nostro possesso.
Pertanto, identificheremo con “y” l’inclinazione del quale siamo ignari del valore e con “y + 10” l’altro angolo sconosciuto e stabiliremo questo legame: y + (y + 10) + 90° = 180°.
Cominciamo con un’operazione di sottrazione, quindi: y + y = 180° – 90° – 10° = 80°.
Dividiamo per 2 e giungiamo alla prima inclinazione alla quale sommiamo 10°, ovvero: [(80 : 2) + 10] = [40° + 10°] = 50°.
Le due inclinazioni saranno quindi di 40° e 50° e la loro totale sarà di 90°.
Chiaramente, l’intoppo illustrato precedentemente è meramente illustrativo. Ma il principio si può implementare senza problemi in situazioni diverse.